阅读paper"一种高效的同态加密方案及其应用"的笔记。

算法的目的是构造一对互逆矩阵, 同时由于每一步中的置换参数都是随机生成的, 所以可使矩阵的
元素不具备任何特征, 可以通过改变随机变换的次数来调整效率和随机性.
来源于BGV方案,作用是将一组密文 - 私钥转换到一组新的密文 -私钥, 同时保证解密正确性.

假设原始的密钥和密文为(S)和(c),则经过密钥交换后输出满足:新密钥和新密文为(S')和(c'=Mc+e approx Mc),其中(e)很小可以忽略,可以看出密钥交换产生的新密文,噪音增加了一点。

其中(I)是(m*m)的单位矩阵。

其中,矩阵(wI)视为明文向量对应的私钥进行了一次密钥转换, 得到公、私钥,所以,假设(wI)对应的明文为(c),(S')对应的明文为(c'=Mc),则:
(w)是什么?也是参数?

加密过程中除计算新密文外, 还引入了一个噪声向量, 从而使得加密结果形式上满足 LWE 问题.

其中(left lceil aright rfloor_q)表示对向量或矩阵(a)中各元素在模(q)的域中取最近整数.(四舍五入)。
为保证解密的正确性, 需要对算法中的各参数做出限制. 下面分析解密过程:

要保证解密正确性需要限制(|Se/w|< 1/2) , 其中符号(|a|)表示向量或矩阵(a)的元素的最大绝对值. 将该限制条件进一步加强, 然后展开得到:

所以噪声(e)的上限:

在该限制条件下, 可以保证解密正确. 在实际应用中, 噪声往往会随着同态计算的进行而不断增大, 而
当噪声足够大时, 就会造成解密失败. 所以在实际应用中, 可以噪音上限的公式中, 得到一个密文可
以进行的同态计算深度(L), 然后再应用中加以限制, 以此来保证同态计算的结果可以顺利解密.(Leveled-FHE)。
1、用同一公钥(M)加密两个等长的明文向量(x_1,x_2)有:
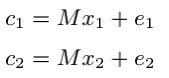
2、将上面两式相加有:

只需给噪声向量 (e_1, e_2)合适的限制条件即可得到:

只要满足:(|S(e_1+e_2)|<1/2),就可以解密正确。
线性变换:给定整数(x),输出(Gx),其中(G)是一个矩阵/向量/整数等,那么如何设计:(Dec(Gc)=Gx)
1、根据解密结构(x=left lceil Sc/wright rfloor_q)可得:(Gx=Gleft lceil Sc/wright rfloor_q=left lceil GSc/wright rfloor_q=Dec(GS,c)),即密文(c)可以看作是明文(Gx)在公钥(GS)下加密的。
2、然后利用密钥交换技术,将(GS)作为输出,得到新密钥(S'),及(M'=Trans(GS)),此时(S')对应的新密文为(c'=M'c+e'),根据密钥交换的性质有:
3、用新密钥(S')对新密文解密:

可以看出上面的噪音不仅有第一次加密时引入的噪声(e), 还有密钥转换过程中引入的新噪声(e')以及因进行线性变换而引入的噪声(|GSe+S'e'|). 将上面解密过程展开有:

所以解密正确的条件是:

随着计算深度的增加噪声的大小也快速增大, 直至无法正确解密.
总结一下流程:
现在给出一个密文(c),想计算其线性变换(Gc),然后解密后相当于对应的明文(x)做线性变换(Gx):
1、将密文(c),对应的私钥(S),变为(GS),作为密钥交换的输入
2、密钥交换输出新私钥(S'),得到新密文(c')
3、用新私钥(S')解密新密文(c')得到明文(Gx)
什么是加权内积?
两向量内积:(<X,Y>=x_1y_1+x_2y_2+...+x_ny_n)
两向量加权内积:(<X,Y,H>=x_1y_1h_1+x_2y_2h_2+...+x_ny_nh_n),其中(H)是权值向量
关于加权内积没看太懂。
回想方案的公私钥{(M,S)}
密钥安全就是不能根据公钥(M)推测出私钥(S)或者在一定程度上模拟出解密过程,即不能仅从公钥和密文就可以解出明文!
观察公钥(M=P_mM_t),是否能从(M)中推断出(P_m)或者(M_t)?
因为(P_m)是一个随机可逆矩阵,想直接构造出(P_m)是困难的。可行的办法就是(P_m^{-1}M=M_t),即需要知道(P_s),可以尝试随机取(P_s),但矩阵规模很大时,很难选取,所以选择合适的矩阵规模,是影响方案安全性的重要参数。
模拟方案是否满足IND-CPA(不可区分的选择明文攻击):

若攻击者能以概率为(Pr=1/2+varepsilon)获胜,则攻击者同样也可以以相同的概率求出(x):
已知$ c_i,M_i,c_i=M_ix+e_i,0 leq i<n$
该问题明显就是LWE问题了,LWE问题被Regev证明是困难的,所以该方案的安全性规约到LWE困难问题上
评论已关闭。