1.0中虽然实现了寻路的算法,但是使用List<>来保存节点性能并不够强
更好的方法是使用堆(或者叫树)来代替列表存储节点
注意:这里使用数组来实现堆,而非使用链表实现堆
这里使用二叉树的方式来存储节点之间的关系
如果在树的末尾添加了一个较小的值,

那么需要和父节点比较大小,如果更小,则交换位置

然后再与父节点比较大小,如果小于父节点,则再次交换位置

如果大于父节点,则停止交换
那如果较小的元素被移除了又怎么排序呢?(之前说过因为Clsot值比较后有时需要重新设置父节点)
首先把树末尾的节点数据添加到树顶
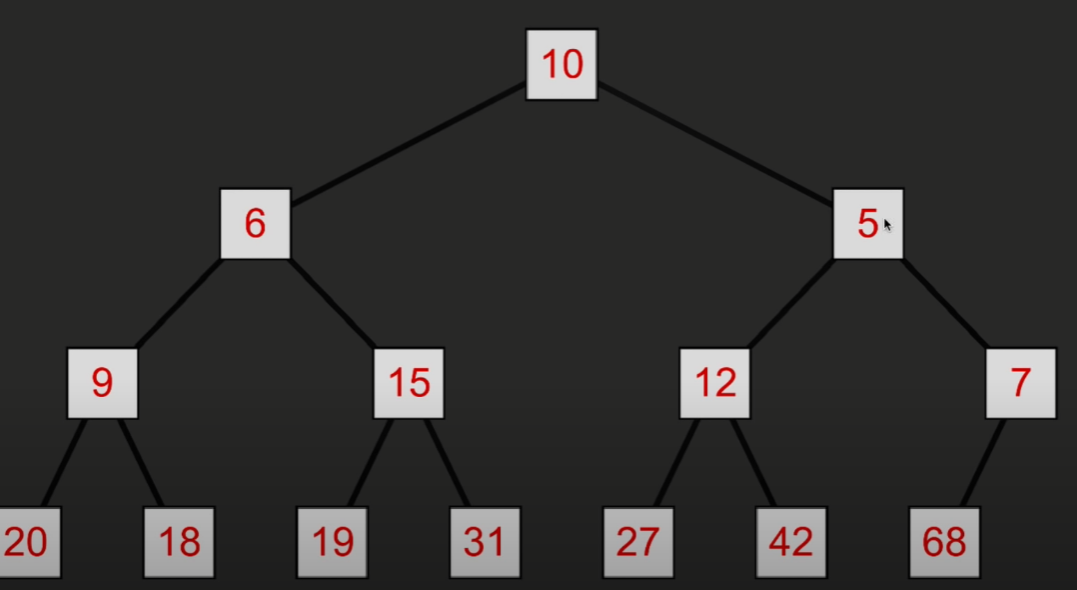
然后与两个子节点比较大小,和更小的那一个交换位置
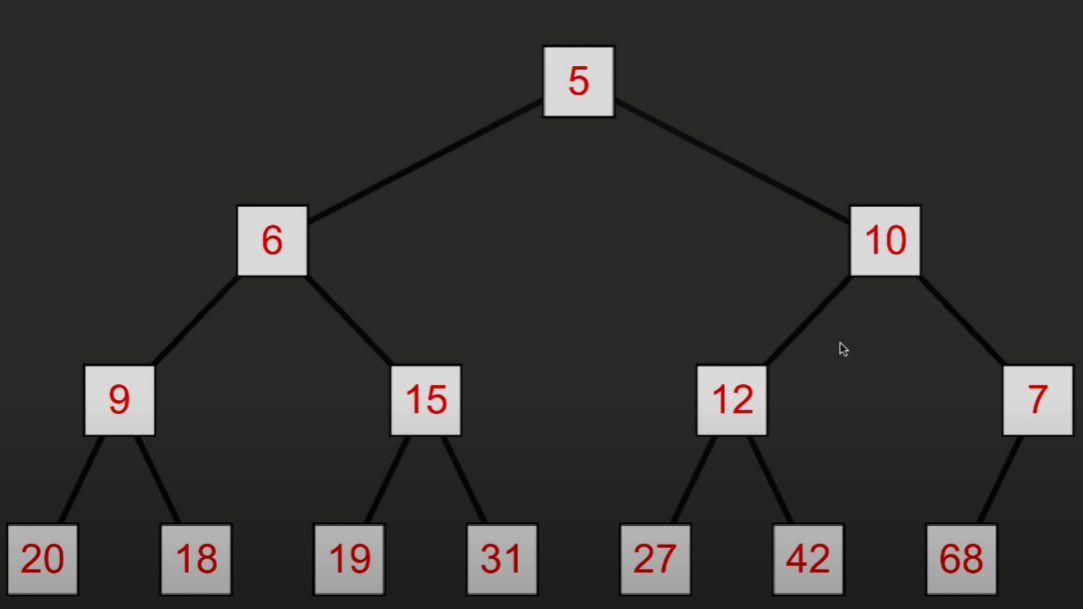
然后再与两个子节点比较大小,直到两个子节点都更大
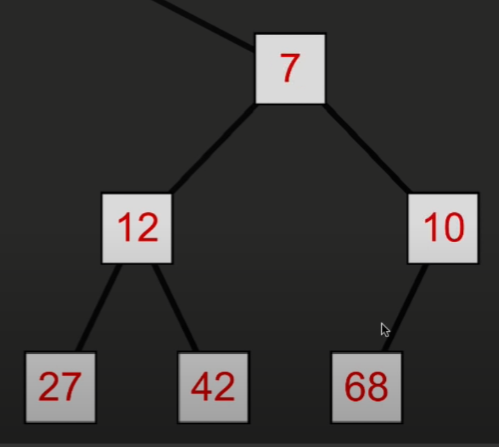
那么如何获取相关的节点呢?这里的数字表示第几个节点而不是存储的具体数据

可以发现以下关系
如果获取某个节点 n (第 n 个节点)
那么该节点的父节点为 ( n - 1) / 2
左子节点为 2n + 1
右子节点为 2n + 2
新建脚本Heap,这是一个数据类型,用来代替List类型,由数组构成
public class Heap<T> where T : IHeapItem<T> //继承了该接口之后,需要实现数据类型T比较大小的方法 { T[] items; //泛型数组,可以为任何类型的数据 int currentItemCount; //当前总共有多少元素 public int Count //属性,访问返回元素个数 { get { return currentItemCount; } } public Heap(int maxHeapSize) //构造器 { items = new T[maxHeapSize]; } public void Add(T item) //添加新元素的方法 { item.HeapIndex = currentItemCount; items[currentItemCount] = item; //末尾添加新元素 SortUp(item); //排序 currentItemCount++; //元素总数+1 } public T RemoveFirt() //获取堆顶部元素并移除 { T firstItem = items[0]; //取得顶部元素 currentItemCount--; //元素总数-1 items[0] = items[currentItemCount]; //将最后一个元素移到顶部 items[0].HeapIndex = 0; //将该元素的索引设为0,即第一个元素 SortDown(items[0]); //下沉元素 return firstItem; //返回取得的顶部元素 } public void UpdateItem(T item) { SortUp(item); } public bool Contains(T item) //判断是否包含元素 { return Equals(items[item.HeapIndex], item); } void SortDown(T item) //下沉元素 { while (true) //一直循环,直到值小于左右子树或到最后位置 { int childIndexLeft = item.HeapIndex * 2 + 1; //左子树的索引 int childIndexRight = item.HeapIndex * 2 + 2; //右子树的索引 int swapIndex = 0; if (childIndexLeft < currentItemCount) // { swapIndex = childIndexLeft; if (childIndexRight < currentItemCount) { if (items[childIndexLeft].CompareTo(items[childIndexRight]) < 0) { swapIndex = childIndexRight; } } if (item.CompareTo(items[swapIndex]) < 0) { Swap(item, items[swapIndex]); } else { return; } } else { return; } } } private void SortUp(T item) //上浮元素 { int parentIndex = (item.HeapIndex - 1) / 2; //父节点的位置 while (true) //循环直至数据比父节点大 { T parentItem = items[parentIndex]; if (item.CompareTo(parentItem) > 0) //如果新的数据比父节点更小(f值更小) { Swap(item, parentItem); //交换位置 } else { break; } parentIndex = (item.HeapIndex - 1) / 2; //下次循环前再次验证父节点索引 } } private void Swap(T itemA, T itemB) //交换数组中两个元素的位置 { items[itemA.HeapIndex] = itemB; items[itemB.HeapIndex] = itemA; int itemAIndex = itemA.HeapIndex; itemA.HeapIndex = itemB.HeapIndex; itemB.HeapIndex = itemAIndex; } } public interface IHeapItem<T> : IComparable<T> //接口,Heap必须实现该接口,IHeapItem继承可比较接口 { int HeapIndex { get; set; } } 接下来是Node
public class Node : IHeapItem<Node> //继承接口,需要实现能够比较Node大小的方法 { ...... private int heapIndex; //声明节点的索引 ...... public int HeapIndex //属性 { get { return heapIndex; } set { heapIndex = value; } } public int CompareTo(Node needToCompare) //实现的比较大小的方法 { //通过比较 F 值的大小,来判断节点的大小 int compare = FCost.CompareTo(needToCompare.FCost); if (compare == 0) { compare = hCost.CompareTo(needToCompare.hCost); } return -compare; } } 接下来是PathFinding
public class PathFinding : MonoBehaviour { ...... private void Update() { if (Input.GetKeyDown(KeyCode.Space)) { //分别注释方法,运行后比较两个方法寻找相同路径所需的时间 //FindPath(seeker.position, target.position); //之前使用List的方法 FindPathHeap(seeker.position, target.position); //新的使用Heap的方法 } } ...... private void FindPathHeap(Vector3 startPos, Vector3 targetPos) { Stopwatch sw = new Stopwatch(); //计时器 sw.Start(); Node startNode = grid.NodeFromWorldPos(startPos); //输入空间坐标,计算出处于哪个节点位置 Node targwtNode = grid.NodeFromWorldPos(targetPos); //这里将List替换为了Heap,初始化Heap Heap<Node> openSet = new Heap<Node>(grid.MaxSize); //用于存储需要评估的节点 HashSet<Node> closedSet = new HashSet<Node>(); //用于存储已经评估的节点 openSet.Add(startNode); while (openSet.Count > 0) //如果还有待评估的节点 { Node currentNode = openSet.RemoveFirt(); //获取其中一个待评估的节点 closedSet.Add(currentNode); //将该节点加入已评估的节点,之后不再参与评估 if (currentNode == targwtNode) //如果该节点为目标终点,就计算出实际路径并结束循环 { sw.Stop(); print("Path found: " + sw.ElapsedMilliseconds + "ms"); RetracePath(startNode, targwtNode); return; } //如果该节点不是目标点,遍历该点周围的所有节点 foreach (Node neighbor in grid.GetNeighbors(currentNode)) { //如果周围某节点不能行走 或 周围某节点已经评估,为上一个节点,则跳过 // 说明某节点已经设置父节点 if (!neighbor.walkable || closedSet.Contains(neighbor)) { continue; } //计算前起始点前往某节点的 gCost 值,起始点的 gCost 值就是0 //经过循环这里会计算周围所有节点的g值 int newMovementCostToNeighbor = currentNode.gCost + GetDinstance(currentNode, neighbor); //如果新路线 gCost 值更小(更近), 或 某节点没有评估过(为全新的节点) if (newMovementCostToNeighbor < neighbor.gCost || !openSet.Contains(neighbor)) { neighbor.gCost = newMovementCostToNeighbor; //计算某节点gCost neighbor.hCost = GetDinstance(neighbor, targwtNode); //计算某节点hCost neighbor.parent = currentNode; //将中间节点设为某节点的父节点 //如果存在某节点gCost更小的节点,会重新将中间节点设为某节点父节点 if (!openSet.Contains(neighbor)) //如果某节点没有评估过 { openSet.Add(neighbor); //将某节点加入待评估列表,在下一次循环进行评估, } } } } } ...... } 接下来是MyGrid
public class MyGrid : MonoBehaviour { public bool onlyPlayPathGizmos; //是否只绘制路径,便于观察 ...... void Start() { nodeDiameter = nodeRadius * 2; gridSizeX = Mathf.RoundToInt(gridWorldSize.x / nodeDiameter); //计算出x轴方向有多少个节点 gridSizeY = Mathf.RoundToInt(gridWorldSize.y / nodeDiameter); //计算出z轴方向有多少个节点 CreateGrid(); } public int MaxSize //属性,返回地图路径点的数量 { get { return gridSizeX * gridSizeY; } } ...... private void OnDrawGizmos() { Gizmos.DrawWireCube(transform.position, new Vector3(gridWorldSize.x, 1, gridWorldSize.y)); if (grid != null) { Node playerNode = NodeFromWorldPos(player.position); if (onlyPlayPathGizmos) { //只绘制路径 if (path != null) { foreach (Node node in path) { Gizmos.color = Color.yellow; Gizmos.DrawCube(node.worldPos, Vector3.one * (nodeDiameter - 0.1f)); } } } else //绘制地图所有点和路径 { foreach (Node node in grid) { ...... } } } } } 接下来为了体现两个方法的耗时差距
修改一下地图的大小和节点的大小

运行结果:
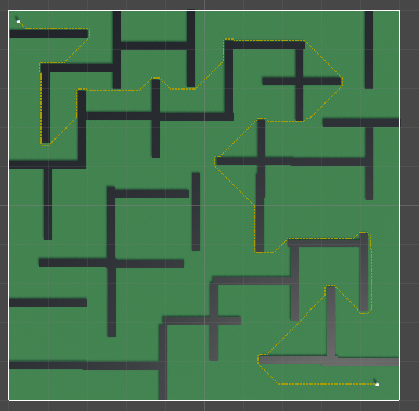
使用Heap的耗时
使用List的耗时

可以看见速度大概提高了三倍
评论已关闭。